▶ 차원의 저주(Curse of Dimensionality)란?
차원의 저주란 학습을 위한 데이터의 차원(=변수의 개수)이 증가하면서 학습데이터의 수가 차원의 수보다 적어져 성능이 저하되는 것을 말합니다. 예를들어, 총 데이터의 수는 200개인데 변수는 700개인 경우가 차원의 저주에 해당합니다. 차원이 높아질수록 데이터 사이의 거리가 멀어지고, 빈 공간이 생기는 공간 섬김 현상(sparsity)을 보입니다.
즉, 간단히 말해 차원이 증가함에 따라 모델의 성능이 안좋아지는 현상인데, 왜 이런 현상이 발생하는 것일까요?
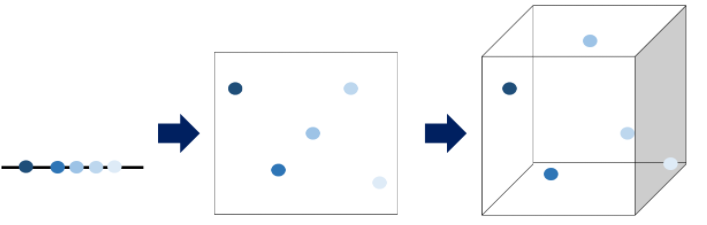
위 그림은 차레대로 1차원, 2차원, 3차원 공간에서의 데이터 분포를 나타냅니다. 1차원인 선의 경우를 보면, 선위에 데이터들이 빽빽하게 나란히 놓여있습니다. 2차원인 평면의 경우는 1차원때보다 데이터들의 간격이 더 벌어져있음을 알 수 있습니다. 3차원인 공간의 경우 점들 사이에 공간이 많이 비어있음을 확인할 수 있습니다. 이처럼 차원이 증가함에 따라, 빈공간이 생기는 것을 차원의 저주라고 합니다.
그렇다면 빈 공간이 생기는 것이 왜 문제가 될까요?
빈 공간이 생겼다는 것은 컴퓨터의 입장에서 그 곳이 0으로 채워졌음을 의미합니다. 이는 정보가 없는 것과 동일합니다. 정보가 적으니 모델이 학습을 할 때 성능이 떨어질 수 밖에 없는 것입니다.
차원의 저주에 가장 치명적인 알고리즘은 KNN(K-Nearest Neighborhood)알고리즘입니다. 이 알고리즘은 자신과 가장 가까이 있는 K개의 이웃 데이터에 따라 분류 결과를 결정합니다. 그런데, 위 그림에서 알 수 있듯이 차원이 커질수록 공간이 생기고 내 주변의 이웃들이 점점 멀어집니다. 따라서 KNN알고리즘은 너무 큰 차원에는 사용을 피하거나, 데이터의 차원을 줄여주는 작업을 거쳐야 합니다.
▶차원의 저주 피하기
차원의 저주를 피하기 위해 차원 축소 기법이 사용됩니다. 가지고 있는 데이터에서 사용할 feature들만 남기는 것입니다. 차원 축소에는 크게 Feature Selection과 Feature Extraction 두 가지 방법이 있습니다.
● Feature Selection : 높은 차원의 feature들 사이에서 상관없는 변수들을 제거하고 의미있는 변수들만 선택하여 남기는 방법입니다. Filtering, Wrapper, Embedded 등이 있습니다.
- Filtering
도움이 되지 않는 feature들을 걸러내는 방법입니다. 통계적인 방법을 이용해 feature들의 상관관계를 알아내고 적합한 feature들만 선택하여 남깁니다. 항상 최적의 feature 부분 집합을 선택할 수는 없습니다.
- Wrapper

예측 모델을 사용하여 feature들의 부분 집합을 만들어 계속 테스트 합니다. 부분 집합을 만드는 방법은 교차 검증을 활용합니다. 테스트 결과를 바탕으로 최적의 feature 집합들을 만듭니다. 최적의 feature들을 찾아내기 위해 여러 번 모델을 생성하고 테스트해아 하기 때문에 시간이 많이 든다는 단점이 있습니다. 또한 Filtering 보다 오버피팅 되기 쉽습니다.
- Embedded

Filtering과 Wrapper를 결합한 방법입니다. 학습 알고리즘 자체에 Feature Selection을 넣는 방식입니다.
● Feature Extraction : 기존 변수들을 조합하여 새로운 feature들을 만들어냅니다. PCA, LDA, SVD, LSA, LLE, MDS, lsomap, t-SNE 등이 있습니다. 이 중 PCA, LDA, SVD, LSA에 대해 자세히 설명해보겠습니다.
- PCA(Principal Component Analysis)
주성분 분석이라고 하며, 고차원의 데이터를 저차원의 데이터로 축소하는 차원 축소 방법입니다. 말그대로 데이터셋이 어떤 성분들로 주로 이루어져 있는지 보고 차원을 축소하는 방법입니다. 비지도 학습 알고리즘에 속합니다. 분산을 최대한 보존하면서 고차원 공간의 데이터를 저차원 공간으로 변환합니다.

위 그림을 보면 2차원 공간에 있는 데이터들이 하나의 주성분을 새로운 축으로 선형변환된 것을 확인할 수 있씁니다. 분홍색 선은 원래 데이터의 분산을 최대한 보존할 수 있는 즉, 데이터가 가장 많이 흩어져 있는 새로운 축입니다. PCA의 목적은 이 축을 찾는데 있습니다.
좀 더 구체적으로 말하자면 입력 데이터의 공분산 행렬을 기반으로 고유 벡터를 생성하고 이렇게 구한 고유 벡터에 입력 데이터를 선형 변환을 거쳐 차원을 축소하는 방법입니다. 차원과 데이터 feature의 수는 동일한 의미를 가지므로 데이터 압축 기법이라고 할 수 있습니다. 또한 PCA는 고유값이 가장 큰, 즉 데이터의 분산이 가장 큰 순으로 주성분 벡터를 추출합니다. 가장 먼저 뽑힌 벡터가 데이터를 더 잘 설명하기도 하고 정보 설명력이 낮은 데이터들은 배제되기 때문에 노이즈 제거 기법이라고도 할 수 있습니다.
- LDA(Linear Discriminant Analysis)
선형 판별 분석이라고 하며 지도학습 알고리즘 입니다. 가장 쉽게 말하면 벡터를 찾는 과정이라고 할 수 있습니다. 찾아야 하는 벡터는 서로 달리 분포하는 데이터 클래스의 차이를 최대화 하고, 클래스 내부의 분포는 최소화하는 벡터입니다. 아래 그림처럼 데이터를 특정한 축에 projection한 후에 두 클래스를 잘 구분할 수 있는 직선을 찾는 것을 목표로 합니다. 그림 속 빨간색과 파란색의 히스토그램은 구한 축을 따라 같은 위치에 있는 점들의 빈도를 세어 나타낸 것입니다.

왼쪽과 오른쪽 그림 중 더 분류가 잘 된 축은 오른쪽입니다. 왼쪽은 중간에 빨간 점과 파란점이 섞여 있고 projection 후 중심이 가깝고 분산이 큰것을 확인 할 수 있습니다. 반대로 오른쪽은 두 점이 서로 섞이지 않았고 projection 후 중심이 멀고 분산이 작습니다. LDA는 이러한 직선을 찾을 수 있도록 해주는 알고리즘입니다.
- SVD(Singular Value Decomposition)
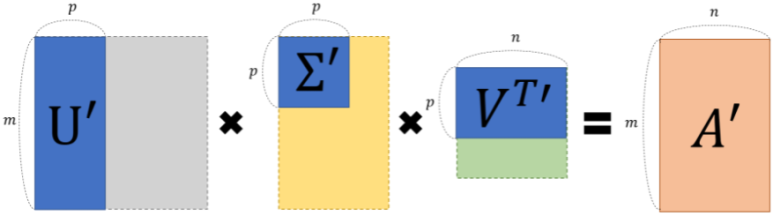
특이값 분해라고 합니다. m*n 크기의 데이터 행렬을 아래와 같이 분해하게 됩니다.

이 방법을 이용해 A라는 임의의 행렬을 A 와 동일한 크기를 갖는 여러 개의 행렬로 분해해서 생각할 수 있습니다. 다시 말해, 임의의 행렬 A를 정보량에 따라 여러 레이어로 쪼개서 생각할 수 있게 해줍니다. 이 특이 값 분해를 차원 축소에 어떻게 이용할 수 있을까요?
기존에 분해된 행렬 A를 특이값 p개 만을 이용해 A'이라는 행렬로 부분 복원할 수 있습니다. 특이값의 크기에 다라 A의 정보량이 결정되기 때문에 값이 큰 몇개의 특이 값들만을 가지고 충분히 유용한 정보를 유지할 수 있게 됩니다.
좀 더 자세한 설명은 이곳을 참조하면 좋습니다!
- LSA(Latent Semantic Analysis)
잠재 의미 분석이라고 합니다. 다변량 통계 분석 방법이며, 고차원 데이터 공간에 대해 축을 변경하여 데이터에 내재해 있는 구조를 밝히는 기법입니다. 축을 찾아내기 위해 앞서 설명한 SVD를 이용합니다.
-t-SNE(t-Distributed Stochastic Neighbor Embedding)
- LLE(Locally Linear Embedding)
- MDS(Multi Dimensional Scaling)
- IsoMap
위 4가지 방법들은 이곳을 참고하면 좋습니다!