Graph Convolutional Network(GCN)는 기존에 영상처리에 많이 사용하던 convolution 연산을 그래프 구조의 데이터에 적용하여, CNN에서 filter의 weight를 여러 feature에 동일하게 sharing하여 작용하도록 한것입니다. 때문에, 그래프에서도 같은 weight값이 여러 노드에 적용되어 노드 분류, 그래프 분류등 다양한 문제를 수행하는 모델입니다.
이 GCN을 사용하여 semi-supervised learning을 하면 그래프의 몇몇 노드에만 레이블이 주어져도 이를 활용하여 나머지 노드의 레이블을 예측할 수 있습니다.
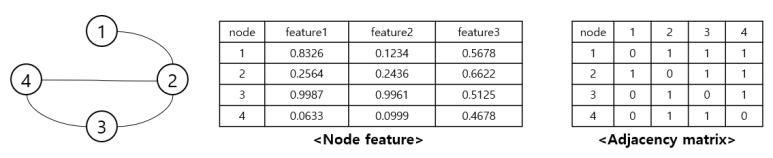
▶ 그래프 구조
먼저 그래프란 노드(vertex)와 간선(edge)의 집합으로 이루어진 자료 구조를 뜻합니다.
각 노드는 그 노드를 나타내는 정보들(node feature)로 포현되고, 노드들 사이의 연결 상태와 관계성에 해당하는 간선은 인접 행렬(adjacency matrix)로 표현합니다.

위 그림처럼 표현되는 그래프 구조의 데이터를 GCN을 이용하여 학습시키는 과정은 아래와 같습니다.
▶ 학습 과정
가장 간단한 방법은 아래 과정을 이용하는 것입니다.


위 그림은 차례대로 A, H, W를 나타냅니다.
괄호안을 먼저 계산하는데 weight의 한 칼럼이 하나의 filter라고 볼 수 있고 이때, 모든 노드가 동일한 weight를 사용하는 것을 알 수 있습니다. 이를 weight sharing이라고 합니다.
괄호안의 연산만 하게 된다면 locality를 고려하지 않은채 연산하게 됩니다. 그러나 이후 인접행렬 A를 곱해주면 주변 노드의 정보만 고려할 수 있는 weighted sum을 하게 됩니다. 각각의 노드와 연결되어 있는 노드의 정보를 모아 feature을 업데이트하는 것입니다.
그러나 이런 방법은 두가지 문제점이 존재합니다.
1. 자기 자신의 feature는 반영되지 않습니다.
- 현재는 이웃 노드의 feature만 합치는 방식이기 때문에 자신의 정보를 포함하지 않습니다.
2. 연결이 많이 되어 있는 노드는 feature representation에서 큰 값을 가지고, 연결이 적은 노드는 값이 작아지게 됩니다.
- 이로 인해 많은 노드와 연결되어 있는 노드에 대한 기울기(gradient)는 폭발하고, (exploding gradient)
- 연결이 적은 노드의 경우 기울기가 소실될 수 있습니다. (vanishing gradient)
- 그렇기 때문에, normalize가 필요합니다.
이러한 문제점을 개성하기 위해 위 식을 다음과 같이 개선하였습니다.

1. 자기 자신을 연결하는 Self-loop 포함해줍니다.
- 인접 행렬 A의 대각선 원소를 1의 값을 가지게 합니다.
- 이렇게 하면, feature을 취합할 때 자신의 feature 또한 포함할 수 있게 됩니다.
2. feature representation 정규화해줍니다.
- 계산된 feature을 정규화(normalize)함으로써 back-propagation을 안정화할 수 있습니다.
- 인접 행렬 A의 차원(D)에 대한 역행렬을 곱해주면 정규화를 할 수 있습니다.
▶ 정리
이미지 2D convolution과 graph convolution은 모두 지역적인 정보를 취합해 feature를 갱신해 나 간다는 공통점이 있습니다. 2D convolution은 특정 pixel과 인접해있는 지역의 정보를 모으지만, graph convolution은 노드와 연결되어 있는 이웃 노드들의 정보를 모은다는 차이점이 존재합니다.
이 때 자신과 연결된 이웃 노드로 부터 정보를 모으는 방법(W matrix)은 한 레이어 안에서 모든 위치, 모든 노드에 대해 공유됩니다.(weight sharing) 이는, 파라미터 수가 적어지기 때문에 Overfitting을 방지할 수 있습니다.
또한, 인접한 이웃 노드로 부터 정보를 받아 Local feature를 학습하기 때문에, 전체 그래프 데이터에 대한 feature를 하나의 뉴런이 가지고 있게 할 수 있습니다.