이번 포스팅에서는 Likelihood(가능도, 우도)와 최대 우도 추정(maximum likelihood)에 대해 설명하겠습니다. Likelihood에 대해 설명하기 전에 Likelihood와 헷갈리는 이름인 Probability(확률)에 대해 간단하게 설명하겠습니다!
- Probability(확률)
확률이란 확률 분포가 주어졌을 때, 특정한 관측 값이나 관측 구간이 확률 분포 안에 얼마나 존재할 수 있을지를 나타내는 값입니다. 핵심은 확률 분포(probability distribution)는 고정하고 그 때의 관측 값 X에 대한 확률 값을 구하는 것입니다. 이를 수식으로 나타내면 아래와 같습니다.
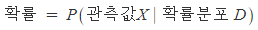
아래 그림으로 설명해보겠습니다.

위 그림의 확률 분포는 쥐들의 몸무게 분포입니다. 종 모양을 이루고 있고 평균 32, 표준편차 2.5를 갖는 정규 분포입니다. 앞서 설명한대로 위 해당 분포를 고정하고 쥐의 몸무게가 32-34 사이로 관측될 확률을 구해보겠습니다. 이는 위 그림에서 빨간 영역과 같게 됩니다. 분포는 고정하고 관측 값에만 변화를 주어 구했습니다.
즉! 확률은 어떤 고정된 분포에서 특정 값 X가 관측될 확률입니다.
- Likelihood(가능도, 우도)
가능도는 확률과 반대되는 개념입니다. 확률에서는 확률 분포를 고정시켰다면 가능도에서는 관측값 X를 고정시킵니다. 어떤 값 X가 관측되었을 때 이것이 어떤 확률 분포로부터 왔을지에 대한 확률입니다. 간단히 애기하면 '확률의 확률'이라고 표현할 수 있을 것 같습니다. 이를 수식으로 나타내면 아래와 같습니다.

확률 설명에서 사용한 그래프를 다시 보겠습니다.
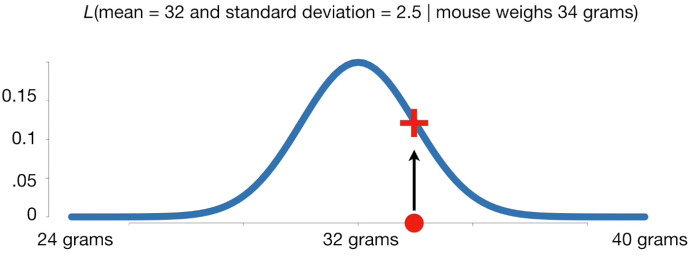
쥐 한마리를 선택해 무게를 쟀을 때 34가 나왔다면 이때 이 관측 결과가 평균 32, 표준편차 2.5를 갖는 정규 분포로부터 왔을 확률은 얼마일까요? 바로 빨간 +가 위치한 약 0.12입니다. 관측 값이 고정되고, 그 관측 값이 주어졌을 때 해당 확률 분포에서 나왔을 확률을 구하는 것입니다.
그럼 이번에 평균 값에 변화를 줘보겠습니다. 몸무게가 34인 쥐가 평균 34, 표준편차 2.5를 갖는 정규 분포로부터 왔을 확률은 얼마일까요?
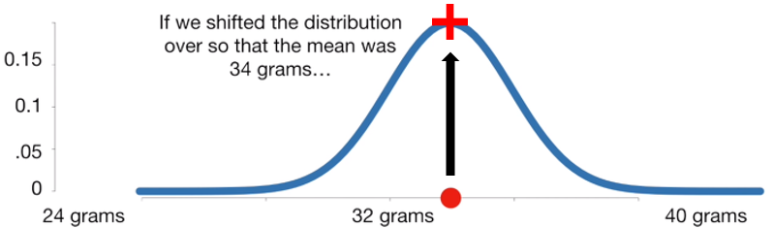
평균 32인 경우에서와 동일하게 구할 수 있습니다. 또한 관측 값이 고정되고 평균이 증가했을 경우 가능도의 값이 높아지는 것도 추가로 확인할 수 있습니다. 이는 몸무게 34인 쥐는 평균 34, 표준편차 2.5에서 더 나올 확률이 크다고 해석할 수 있습니다.
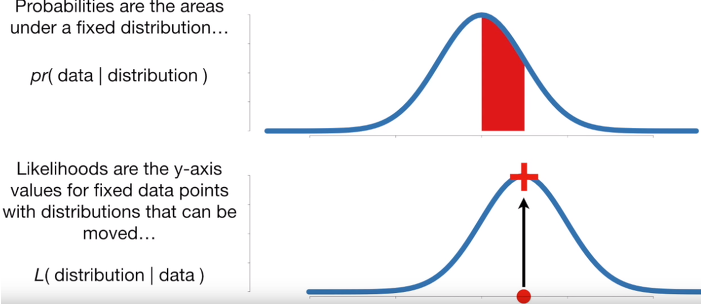
※ 요약!
확률 : 주어진 확률 분포에서 관측 값 X가 나올 확률
가능도 : 주어진 관측 값 X에서 이것이 어떠한 확률 분포로 부터 나올 확률
- 최대 우도 추정(maximum likelihood)
최대 우도 추정은 각 관측 값에 대해 총 가능도가 최대가 되게 하는 분포를 찾는 것입니다. 예를 들어 설명해보겠습니다. x={1, 4, 5, 6, 9} 이렇게 5개의 데이터를 얻었다고 가정하겠습니다.
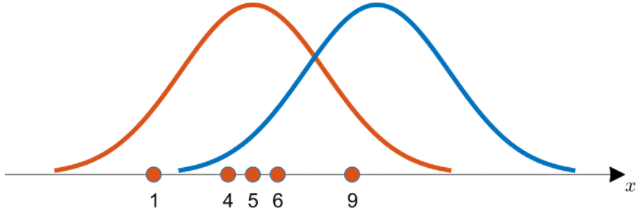
이 데이터를 직선에 옮기고 주황색과 파란색 두 개의 정규분포 그래프를 그려보겠습니다. 두 그래프 중 어떤 그래프로 부터 추출되었을 확률이 높을까요? 데이터의 분포가 주황색 그래프의 중심과 더 가깝기 때문에 우리는 주황색 그래프로 부터 추출되었다고 추정해볼 수 있습니다.
좀 더 구체적으로 수학적인 방법을 이용하여 접근해보도록 하겠습니다.
가능도에 대해 다시 설명하자면, 가능도는 관측 값이 어떠한 확률 분포로부터 나왔을 확률을 말합니다. 가능도를 계산하기 위해서는 각 데이터 샘플에서 후보 분포에 대한 높이를 계산해서 다 곱하는 방법을 이용할 수 있습니다. 곱셈을 이용하는 이유는 데이터들의 추출이 독립적으로 연속하여 일어나기 때문입니다. 이제 이 값이 각 확률 분포에 대해 관측 값들의 가능도를 구해 그 곱이 최대가 되면 됩니다. 이를 수식으로 유도하면 아래와 같은 과정을 거칩니다.
먼저, 가능도 함수를 수식으로 쓰면 아래와 같습니다. x는 관측 값, θ는 분포를 의미합니다.
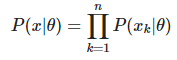
그 다음 log를 씌워줍니다.
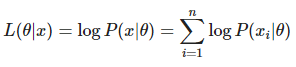
마지막으로 위 식에서 최대값을 찾아주면 됩니다. 최대값을 찾을 때는 미분 계수를 이용합니다. 경사하강법에서 최소가 되는 지점을 찾기 위해 미분을 하는 것과 같은 원리입니다.
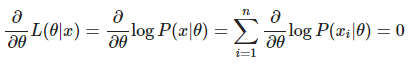
θ에 대해 편미분을 하고 그 값이 0이 되도록 하는 θ를 찾는 과정을 통해 가능도 함수를 최대로 만들어 주는 분포 θ를 찾을 수 있습니다.
'AI Research > Artificial Intelligence' 카테고리의 다른 글
| [인공지능 기초] 차원의 저주(Curse of Dimensionality) (0) | 2023.03.05 |
|---|---|
| [인공지능 기초] EM Clustering (0) | 2023.02.28 |
| [인공지능 기초] 결측치(Missing Value) 처리 (0) | 2023.02.28 |
| [인공지능 기초] 머신러닝 분류모델 정리 (0) | 2023.02.28 |
| [인공지능 기초] 나이브 베이즈 분류(Naive Bayes Classification) (0) | 2023.02.28 |