이번 게시물에서는 이전 게시물에 이어 다양한 Convolution 기법들에 대해 작성합니다!
5. Depthwise Separable Convolution
앞서 설명했던 depthwise convolution은 하나의 kernel이 하나의 채널에만 연산을 하고 각각의 연산 결과를 하나로 모으는 방식이었습니다. 이와 달리 Depthwise Separable Convolution은 각 채널의 출력 값들이 하나로 합쳐지는 방식입니다.
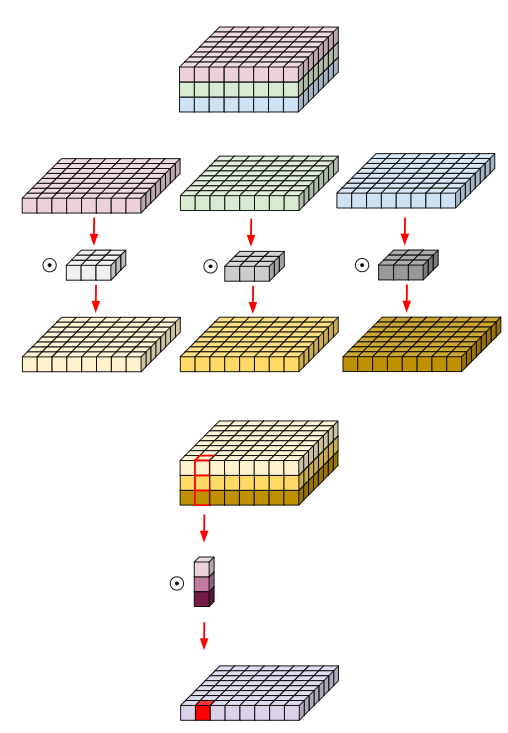
depthwise convolution은 채널들끼리 정보 교류가 없었지만 Depthwise Separable Convolution은 spatial feature와 channel-wise feature 를 모두 고려하기 때문에 채널간 정보교류를 하며 네트워크를 경량시킬 수 있습니다. 역시 기존의 Convolution보다 연산량이 훨씬 적다고 합니다. Pytorch로는 아래와 같이 구현될 수 있습니다!
class depthwise_separable_conv(nn.Module):
def __init__(self, nin, kernels_per_layer, nout):
super(depthwise_separable_conv, self).__init__()
self.depthwise = nn.Conv2d(nin, nin * kernels_per_layer, kernel_size=3, padding=1, groups=nin)
self.pointwise = nn.Conv2d(nin * kernels_per_layer, nout, kernel_size=1)
def forward(self, x):
out = self.depthwise(x)
out = self.pointwise(out)
return out
6. Pointwise Convolution
depthwise convolution이나 Depthwise Separable Convolution과 다르게 pointwise convolution은 spatial 방향의 convolution은 진행하지 않고 채널 방향의 convolution만 진행합니다. 때문에 앞선 2개의 convolution은 입출력 채널수가 동일해야 했지만 Pointwise Convolution은 채널수를 조정할 수 있어서 channel reduction에 이용할 수 있습니다.
위 그림은 1*1 커널로 Pointwise Convolution을 진행하는 과정입니다. 1*1*C 크기의 kernel을 사용함으로써 feature map의 여러 채널을 하나의 채널로 압축해버릴 수 있습니다. 이는 하나의 kernel이 채널별로 coefficient를 가지는 linear combination을 표현한다고 할 수 있습니다. 중요도가 낮은 채널은 linear combination 시에 낮은 coefficient를 갖도록 학습됩니다. 그리고 다채널의 feature map을 더 적거나 많은 채널의 feature map으로 embedding 할 수도 있다는 의미가 되기도 합니다.
출력 채널수를 감소시킨다면 계산량과 파라미터수를 줄여 연산속도가 향상되지만, 데이터 압축에 따른 정보손실또한 필수적으로 따라오기도 합니다. 때문에 속도와 정보손실의 trade-off를 잘 고려하여 적절한 방식을 선택해야 합니다. Pytorch로는 아래와 같이 구현될 수 있습니다!
class pointwise_conv(nn.Module):
def __init__(self, nin, nout):
super(depthwise_separable_conv, self).__init__()
self.pointwise = nn.Conv2d(nin, nout, kernel_size=1)
def forward(self, x):
out = self.pointwise(x)
return out
7. Grouped Convolution
Grouped Convolution은 입력 feature map의 채널들을 여러 개의 그룹으로 묶어 각 그룹별로 convolution 연산을 수행하는 방법입니다. 각 그룹별로 한번에 병렬처리를 진행해 빠른 연산이 가능합니다.

각 그룹에 영향을 많이 끼치는 (==높은 correlation을 갖는 ) 채널이 더 중점적으로 학습 될 수 있다는 장점이 있습니다. 결과적으로 각 그룹마다 독립적으로 필터가 학습되길 기대할 수 있습니다.
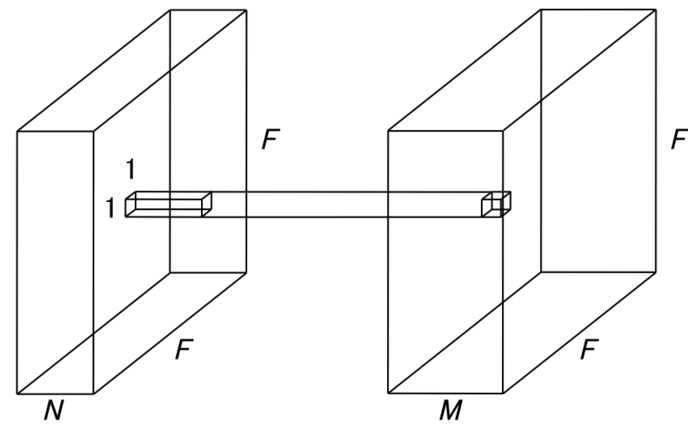
그룹수는 하이퍼 파라미터로 직접 조정해줄 수 있습니다. 적당한 수의 그룹은 파라미터 수는 감소하면서 성능이 향상되는 장점이 있지만 너무 많은 그룹으로 분할하면 오히려 성능이 감소할 수 있습니다. 아래는 Grouped Convolution의 파라미터수를 나타냅니다.

K = 필터크기, N = 출력채널크기, M = 입력채널크기, g = 그룹 개수입니다. 원래의 Convolution 연산의 파라미터 수가 K^2NM인 것과 비교했을 때 훨씬 작은 파라미터수를 갖습니다. Pytorch에서 사용하려면 아래 groups 파라미터를 원하는 수로 설정해주면 됩니다.
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)
8. Deformable Convolution
Deformable Convolution은 말 그래도 정형화 되지 않은 , 변형 가능한 Convolution입니다. "Deformable Convolutional Networks"논문에서 제안하였습니다. 기존 Convolution의 단점 중 하나는 늘 고정되어 있다는 점입니다. Object Detection을 예로 들어보자면 , 이미지 속에 등장하는 물체들의 크기는 너무나도 다양한데, 적용되는 kernel의 크기는 늘 일정하여 receptive field 또한 일정하다는 한계가 있습니다. 이는 복잡한 transformation에 적용하기에는 적합하지 않습니다.
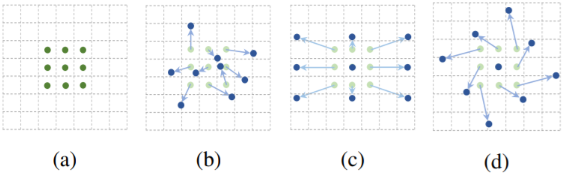
위 그림의 (a)는 일반적인 Convolution을 (b), (c), (d)는 다양한 패턴으로 변형시킨 Convolution 입니다. scale, 종횡비, 회전 방식등을 조절하여 다양하게 변형할 수 있습니다. 아래 그림은 Deformable Convolution의 그림입니다.
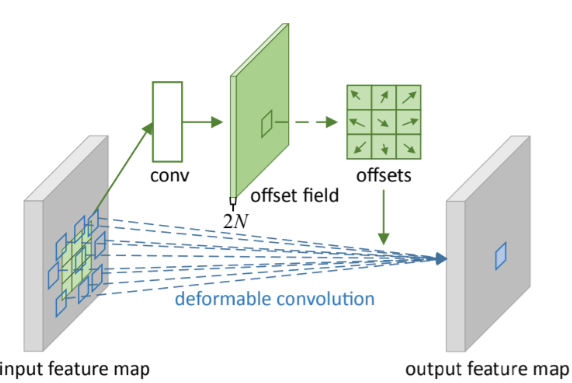
기존 Convolution과 비교하여 offset field가 추가되었습니다. 이 부분은 각 입력의 2D offset을 학습하기 위한 것으로 소수값도 가능합니다. filter size를 학습하여 다양한 formation에 적절히 대응할 수 있도록 합니다. 학습 결과를 확인해보겠습니다.

convolution filter의 예시를 보여주는 그림입니다. 빨간 점은 위의 offset을 반영한 sampling location이고 초록 점은 filter의 output 위치입니다. 한 이미지의 물체들 마다 크기가 고정되지 않고 큰 물체에서는 크게, 작은 물체에서는 작게 receptive field가 변화하는 것을 확인 할 수 있습니다. Deformable Convolution의 official github은 여기에, pytorch 로 구현된 github은 여기로 가시면 됩니다!
본 포스팅은 아래의 글들을 참고하여 작성하였습니다 :)
https://zzsza.github.io/data/2018/02/23/introduction-convolution/
https://eehoeskrap.tistory.com/431
'AI Research > Deep Learning' 카테고리의 다른 글
| [딥러닝 기본지식] Auto Regressive Models (0) | 2023.05.07 |
|---|---|
| [딥러닝 기본지식] Diffusion Model (0) | 2023.05.01 |
| [딥러닝 기본지식] 다양한 Convolution 기법_with Pytorch (1) (0) | 2023.04.22 |
| [딥러닝 기본지식] 딥러닝 프레임워크 비교(Tensorflow, Keras, Pytorch) (0) | 2023.03.04 |
| [딥러닝 기본지식] Transfer Learning과 Fine Tuning (0) | 2023.03.04 |