Regularization과 Normalization은 딥러닝에 자주 등장하는 단어입니다. 이번 포스팅과 다음 포스팅에서는 두 단어의 개념에 대해서 설명하도록 하겠습니다.
▶ Regularization
번역하여 '일반화'라고 이해하면 쉽게 이해 할 수 있을 것 같습니다. 이 방법은 모델에 제약(패널티)을 줘 오버피팅을 해결하는 방법이라고 할 수 있습니다. perfect fit을 포기하여 training acccuracy(학습 정확도)를 낮춤으로써 모델을 더 일반적이게(generalization) 만드는 것입니다. 그 결과로 potential fit이 증가하게되고 testing accuracy를 높힐 수 있습니다.
모델을 만드는 방법 중 가장 단순한 것은 계속해서 loss function의 값이 작아지는 방향으로만 진행하는 것입니다. 그러나 이 방법은 특정 가중치가 너무 큰 값을 가지게 되므로 일반화 성능이 떨어지게됩니다. 위 그림에서 actual function이 실제 학습을 통해 얻어야하는 함수라고 했을 때 왼쪽 그래프의 model(빨간선)은 모든 학습 데이터에 대해 완벽하게 피팅되었습니다. 즉, 오버피팅이 일어난 상태입니다. 그렇기 때문에 일반적으로 적용했을 때 올바른 정답을 내지 못합니다. Regularization은 이러한 일이 발생하지 않도록 학습시에 가중치에 제약을 걸어 오른쪽 그래프처럼 만들어 주는 것입니다. 대표적인 방법으로는 L1 Regularization과 L2 Regularization이 있습니다.
L1 Regularization와 L2 Regularization에 대해 설명하기 전에 알아야할 개념들에 대해 먼저 설명 하겠습니다.
● Norm
Norm은 벡터의 크기(길이)를 측정하는 방법입니다. 두 벡터 사이의 거리를 측정하는 방법이기도 합니다. 그 중하나가 바로 절댓값입니다. |(1,2)|처럼 나타낼 수 있습니다. Norm의 정의는 다양하고 복잡하지만 결국 어떤 값의 크기를 계산하고, 비교 가능한 값으로 만드는 함수 정도로 생각하면 됩니다. 수식으로 나타내면 아래와 같습니다.
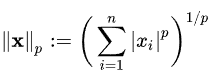
위 식에서 p는 Norm의 차수를 의미합니다. p가 1이면 L1 Norm이 되는 것이고, 2면 L2 Norm입니다.

L1 Norm과 L2 Norm
- L1 Norm : Manhattan Distance, Taxicab geometry라고도 합니다. 위 그림에서 알 수 있듯이 두 개의 벡터를 빼고 절대값을 취한 뒤 합한 것입니다. 수식으로 나타내면 아래와 같습니다.

(3,1,-3)과 (5,0,7) 두 개의 벡터가 있다면 L1 Norm은 |3-5| + |1-0| + |-3-7|=13이 됩니다.
- L2 Norm : Euclidean distance라고도 합니다. 두 개의 벡터의 각 원소를 빼고, 제곱을 해 더하고 루트를 씌운 것입니다. 수식은 아래와 같습니다.

(3,1,-3)과 (5,0,7) 두 개의 벡터가 있다면 L2 Norm은 root(4+1+100)=root(105)입니다.
=> L1 Norm과 L2 Norm의 차이

검정색 두 점 사이의 거리는 다양하게 표현될 수 있습니다. 위 그림의 빨, 파, 초, 노 선은 수 많은 거리들 중 하나입니다. 이중 빨간색, 파란색, 노란색 선은 L1 Norm을 의미하고, 초록색은 L2 Norm을 나타냅니다. 즉, L1 Norm은 여러가지 일 수 있지만, L2 Norm은 가장 짧은 경로 하나만 가집니다.
● L1 Loss

L1 Norm을 기준으로 만들어진 L1 Loss 함수입니다. Least Absolute Deviations(LAD), Least Absolute Errors(LAE), Least Absolute Value(LAV), Least Absolute Residual(LAR) 등 다양하게 불립니다. 두 개의 벡터가 들어간 자리에 모델 입력 데이터의 실제 값(y_true)과 예측 값(y_prediction)을 넣어주면 됩니다. 실제 값과 예측치 사이의 오차의 절대값을 구하고 그 오차들의 합을 의미합니다.
L1 Loss는 L2 Loss보다 이상치의 영향을 덜 받고, Robust(덜 민감)하지만 0에서 미분이 불가능하다는 단점이 있습니다.
● L2 Loss

L2 Norm을 기준으로 만들어진 L2 Loss 함수입니다. Least Squares Error(LSE, 최소자승법)로도 불립니다. L1 Loss와 달리 제곱을 취하기 때문에 이상치가 들어오면 오차가 제곱이 되어 더 커져서 이상치에 영항을 더 많이 받게됩니다.
● L1 Regularization

L1 Norm, L1 Loss 처럼 절대값을 이용합니다. 식의 가장 마지막 부분에 가중치에 절대값을 씌운 것을 확인할 수 있습니다. 기존의 손실 함수에 가중치 크기(패널티)가 포함되면서 loss가 더 커지게 만드는 것인데, 가중치의 과도한 변화를 막고 너무 크지 않은 방향으로 학습되도록 해줍니다. 위 식을 편미분하면 w 값은 상수가 되고, 그 부호에 땨라 +,- 가 결정됩니다. 가중치가 너무 작은 경우에는 상수 값(λ)에 의해 weight가 0이 되버리고 결국 중요한 몇몇 가중치들만 남게됩니다. 즉, 불필요한 feature에 대응하는 weight를 정확히 0으로 만들어서 feature selection의 효과를 냅니다.
● L2 Regularization

식에 제곱값이 포함된 것을 확인할 수 있습니다. 기존의 손실 함수에 가중치의 제곱을 포함하여 더함으로써 마찬가지로 가중치가 너무 크지 않은 방향으로 학습되도록 해줍니다. 이 방법은 loss 뿐만 아니라 가중치 또한 줄어드는 방식으로 학습을 합니다. 특정 가중치가 비이상적으로 커지는 것을 방지하고, weight decay가 가능해집니다. 전체적으로 가중치를 작게하여 과적합을 방지하는 것입니다. 불필요한 feature에 대응하는 weight를 0에 가깝게 만듦으로써 L1 Regularization에 비해 일반화 능력을 향상 시키는 것으로 알려져 있습니다.
=> L1 Regularization와 L2 Regularization의 차이
L1 Norm과 L2 Norm의 차이에서 설명했듯이 L1 Norm은 여러 경로가 존재하고, L2 Norm은 가장 짧은 거리 한개만 존재했습니다. 다시 말하면, 다양한 L1 Norm은 feature를 선택하는 것이 가능하다고 할 수 있습니다. L1 Regularization 또한 여기에 기반을 두기 때문에 동일하게 적용 될 수 있습니다. 이러한 특징 때문에 L1 Regularization은 sparse모델에 적합합니다.
'AI Research > Artificial Intelligence' 카테고리의 다른 글
| [인공지능 기초] 선형 회귀(Linear Regression)와 로지스틱 회귀(Logistic Regression) - 1 (0) | 2023.02.28 |
|---|---|
| [인공지능 기초] 정규화 (Normalization) (0) | 2023.02.26 |
| [인공지능 기초] 랜덤 포레스트(Random Forest) (0) | 2023.02.26 |
| [인공지능 기초] 결정 트리(Decision Tree) (0) | 2023.02.26 |
| [인공지능 기초] 앙상블 학습(Ensemble Learning) (0) | 2023.02.26 |
