▶ 가중치(weight)
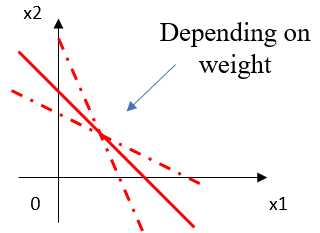
각 입력 신호가 결과 출력에 미치는 중요도를 조절하는 매개변수(parameter)입니다. 입력 값에 곱해지는 수이며, 입력으로 들어온 데이터들 중에서 어떤 feature를 많이 반영하고, 어떤 feature를 덜 반영할지 결정해줍니다. 가중치는 활성화 함수에 따라 기울기를 증가시킵니다. 가중치가 커질 수록 그 feature는 모델에 더 많은 영향을 미치게 됩니다.
예를 들어, 집값을 예측하는 모델이 있다고 가정하겠습니다. 입력으로 들어오는 feature는 역과의 거리, 방 넓이, 층 수, 창문의 개수 등이 있습니다. 이 중 창문의 개수는 다른 세 개의 feature에 비해 덜 중요합니다. 따라서 역과의 거리, 방 넓이와 층 수는 높은 가중치를 창문의 개수는 낮은 가중치를 가지도록 학습됩니다.
▶ 편향(bias)
뉴런의 활성화 조건을 결정하는 매개변수입니다. 활성화 함수에서 설정된 임계값을 얼마나 쉽게 넘게 할 것인지 결정해줍니다. 편향이 높다면 그만큼 활성화 함수의 임계값을 넘기 어렵기 때문에 까다로운 모델이 됩니다. 활성화 함수의 임계값을 넘지 못하면 그 뉴런은 활성화되지 못하기 때문에 간단한 모델이 됩니다. 반대로 편향이 작으면 활성화되는 뉴런이 많아져 복잡한 모델이 됩니다.
이전 포스팅들에서 설명했다시피 활성화 함수는 0을 기준으로 x가 음수 값일때 0또는 음수값의 출력을 내고 x가 양수값일때 양수 값의 출력을 냅니다. y=wx+b라는 함수가 있다고 했을 때 wx+b가 양수가 되어 뉴런에 활성화를 일으키고 싶다면 b가 wx보다 커야 할 것입니다. 바꿔 말하자면 이는 위에 설명한대로 편향이 높아활성화 함수의 임계값을 넘기 어렵다는 뜻이 됩니다. 활성화를 시키고싶지 않은 경우에도 동일합니다.
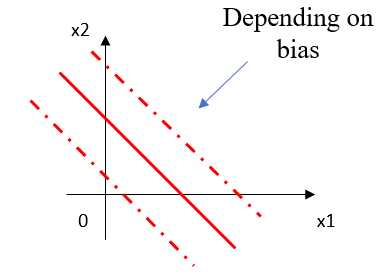
아래 그림에서 확인할 수 있듯이 모델의 결정 경계의 위치를 수평적으로 변경합니다.
▶ 예제로 살펴보기
아래와 같이 3개의 입력을 받는 모델이 있다고 하겠습니다.
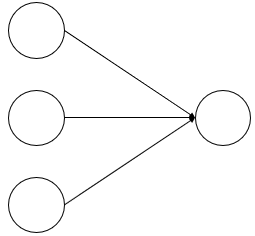
각 입력 데이터의 값과 가중치를 설정해보겠습니다. 검은색 숫자는 입력 값을 빨간색 숫자는 가중치 입니다.
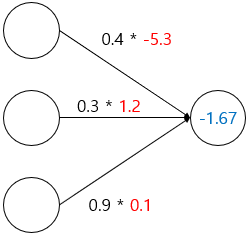
자세히 보면, 첫번째 뉴런의 가중치는 -5.3으로 다른 뉴런들과 절댓값으로 비교해보았을 때 매우 큰 값을 가집니다. 때문에 -1.67이라는 출력을 내는데 가장 큰 역할을 합니다. 마지막 뉴런은 0.9라는 가장 큰 입력 값을 받았지만 가중치가 0.1로 가장 작아 뉴런의 출력값 또한 0.09로 미미해지는 것을 알 수 있습니다.
이 모델에 편향을 추가해보겠습니다.
편향 값 -1.3과 4를 추가해보겠습니다.
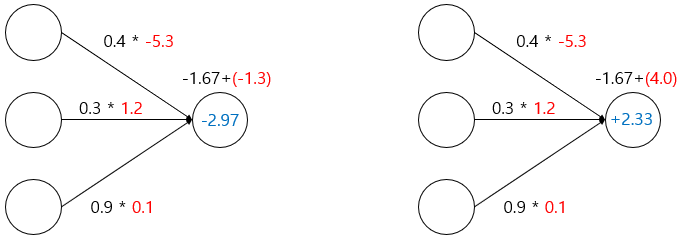
각각 -2.97과 2.33이라는 값이 나왔습니다. 활성화 함수로 로지스틱 회귀 함수를 사용하여 두 값을 통과 시켜 보겠습니다. 로지스틱 회귀 함수는 아래와 같은 식을 갖습니다.
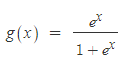
위 활성화 함수에 통과시키면 각각 0.0488와 0.9512이라는 값이 나옵니다. 편향의 값이 -1.3에서 4로 바뀌었을 뿐인데 0에 가깝던 값이 1에 가까운 값으로 변하였습니다. 같은 가중치를 가져도 편향 값에 따라 최종 출력은 다양해지기 때문에 뉴런의 활성화 조건을 결정해줄 수 있습니다.
'AI Research > Deep Learning' 카테고리의 다른 글
| [딥러닝 기본지식] Transfer Learning과 Fine Tuning (0) | 2023.03.04 |
|---|---|
| [딥러닝 기본지식] 그래프 신경망(Graph Neural Network) (0) | 2023.03.04 |
| [딥러닝 기본지식] 평가 지표(Metrics) (0) | 2023.03.04 |
| [딥러닝 기본지식] 오차 역전파(backpropagation)의 이해 - 계산그래프와 연쇄법칙(chain rule) (1) | 2023.03.04 |
| [딥러닝 기본지식] 최적화 함수(optimizer)의 이해 - 최적화 함수의 정의와 다양한 종류들 (0) | 2023.03.03 |