▶ Graph Neural Network(GNN)
GNN은 그래프 구조의 데이터를 입력으로 사용하는 인공 신경망입니다. 가장 많이 쓰이는 인공 신경망들인 FCN(Fully Connected Network)과 CNN(Convolutional Neural Network), RNN(Recurrent Neural Netwrok)등은 보통 벡터나 행렬 형태의 입력을 사용합니다. 그에 비해, GNN은 입력이 그래프 구조입니다.
▶ Neighborhoods Aggregation
GNN은 입력으로 그래프 구조(노드들 사이의 연결 상태)와 노드별 feature 정보를 받습니다. 입력으로 받은 feature들의 정보와 이웃 노드 정보를 바탕으로 각 노드 별 embedding 을 출력 결과를 얻을 수 있습니다. 이때 벡터 형태로 출력됩니다. 예를 들어, 노드 A가 이웃 노드로 B, C, D를 갖고 GNN이 하나의 레이어로 이루어져 있다고 할 때, A의 embedding은 현재 A의 feature와 함께 이웃 노드인 B, C, D의 feature에 의해 결정됩니다.

CNN에서 인접 픽셀의 정보를 사용하는 필터처럼, GNN에서는 인접한 노드들의 정보를 함께 사용하는 구조라고 생각할 수 있습니다.
위의 그림에서는 레이어를 하나만 두었지만 여러 개 쌓으면 깊은 신경망을 쌓아 딥러닝 작업을 할 수 있게 됩니다. 레이어를 두개 쌓으면 어떻게 될까요? 레이어 두개를 거치고 난 후의 노드 A의 embedding feature는 이웃 노드인 B, C, D와 A의 첫번째 레이어를 거친 후의 embedding 값에 의해 결정됩니다.
그럼 GNN은 어떻게 자기 자신의 정보와 이웃들의 정보를 합쳐 새로운 embedding값을 만들어내는 것일까요? 대략적인 과정은, 먼저 이웃들의 정보를 모으고, 모은 정보를 통해 만들어낸 새로운 값과 이전 상태의 자기 자신의 값을 이용해 새로운 embedding값을 얻습니다. 두 값을 합치는 과정으로 Concat(연결연산)이 이용됩니다.

▶ GNN의 학습 및 활용
위 그림에서 알 수 있듯이 한 노드의 feature 업데이트 과정은 이웃 노드의 정보를 모으는 AGGREGATE 함수와 CONCAT 함수를 통해 이루어집니다. 서로 다른 층의 AGGREGATE 함수는 각기 다른 함수이며, 각 정점마다 이웃 노드가 다르므로 같은 AGGREGATE 함수를 사용하더라도 입력의 수가 다를수 있습니다. 따라서, AGGREGATE 함수는 서로 다른 구조의 그래프를 처리할 수 있어야 합니다. 이 두 함수의 학습과정은 어떻게 될까요?
일반적인 신경망의 학습과정은,
1. 학습한 신경망의 구조를 정합니다.
2. 손실 함수(loss function)와 최적화 함수(optimizer)를 결정합니다.
3. 2번에서 정의한 함수를 사용해 손실이 0에 가까워지도록 weight를 학습합니다.
GNN의 학습과정도 유사합니다.
1. AGGREGATE 함수와 CONCAT 함수를 정합니다.
2. 손실 함수(loss function)와 최적화 함수(optimizer)를 결정합니다.
3. 2번에서 정의한 함수를 사용해 AGGREGATE 함수와 CONCAT 함수 손실이 0에 가까워지도록 weight를 학습합니다.
그래프 신경망은 다양한 분야에 사용될 수 있습니다.
첫번째로 Node Classification문제에 사용할 수 있습니다. 지도 학습(supervised learning)인 경우에 각 노드가 어떤 클래스인지 분류할 수 있는 데이터를 주면 됩니다. 학습 방법도 일반 적인 분류 문제와 동일합니다. 손실함수 또한 분류 문제에서 많이 사용할 수 있는 cross entropy loss를 사용하면 됩니다.
또한 비지도 학습(unsupervised learning)인 문자열 각 단어의 embedding을 구하는 word2vec와 같은 작업에서도 그래프 구조를 사용하여 각 노드의 embedding feature를 구할 수 있습니다.
마지막으로 그래프를 전체를 분류하는 문제에도 사용할수 있습니다. 이 경우에는 마지막 레이어까지 거친 후 모든 노드의 feature를 하나로 모아 그래프 전체가 어떤 클래스에 속하는지 분류하는 방식으로 이루어집니다. 화학 구조식을 입력으로 주고 독성을 가지는지, 아닌지를 판별하는 문제가 이에 해당합니다.
▶ 다양한 GNN들
기본 GNN에서 조금씩 변형된 다양한 GNN들을 소개하겠습니다.
기본적인 AGGREGATE 함수는 결과를 이웃들의 이전 레이어의 embedding의 평균이 되도록 정의할 수 있습니다. hkv는 k번째 레이어를 거친 후 v의 embedding feature를 나타냅니다. 이 경우 hkv는 아래와 같이 나타낼 수 있습니다.

각각의 k에 대해 W와 B는 학습 가능한 파라미터가 되고, 이러한 파라미터를 최적화 하는 방향으로 학습이 진행됩니다. '+'를 기준으로 앞부분은 이전 레이어에서 계산한 이웃들의 임베딩 평균을 선형변환하는 부분이며, 뒷 부분은 이전층에서의 자기 자신 노드의 embedding을 선형변환 하는 부분입니다.
● 그래프 합성곱 신경망(Graph Convolutional Network, GCN) - 자세한 설명 보러가기!
위 AGGREGATE 함수와 크게 다르지 않지만 Neighborhood aggregation을 조금 다르게 변형하여 성능을 개선하였습니다. GCN에서 hkv를 구하는 식은 아래와 같습니다.
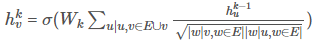
기본적인 AGGREGATE 함수와의 차이점은 크게 두가지가 있습니다.
- 이웃들은 aggregate할 때 W를 사용하고, 자기 자신의 이전 embedding에는 B를 곱했는데, GCN에서는 자기 자신과 이웃에 대해 동일한 parameter인 W를 사용합니다.
- 단순히 이웃들의 embedding 평균을 구하는 것과 다르게 이웃들끼리 aggregate할 때 normalization를 적용해 차등적으로 반영할 수 있도록 하였습니다. 예를 들어, v의 이웃노드로 u와 w 두개의 정점이 있을 때, u가 w보다 다른 노드와 더 많이 연결되어 있다면(= 차수가 크다면) embedding 레이어를 거친 후 embedding을 결정하는데 w가 더 많은 영향을 끼칩니다.
● Graph Sample and aggregate(GraphSAGE)
역시 Neighborhood aggregation을 조금 다르게 변형하여 성능을 개선하였습니다. GraphSAGE에서는 AGGREGATE 함수 후보로 아래 세 가지를 제안했습니다.
- Mean aggregator: 기본적인 AGGREGATE 함수와 동일합니다.
- LSTM aggregator: RNN계열의 신경망 중 하나인 LSTM을 이용해 aggregate하는 방법입니다. 그래프에서 이웃 노드들 사이에 순서를 정할 수 있는 방법은 없기에 random permutation을 사용하여 순서를 정하고 LSTM의 입력으로 사용합니다. LSTM의 출력이 AGGREGATE 함수의 최종 결과가 됩니다. 이웃들의 순서에 따라 결과가 달라집니다.
- Pooling aggregator: 각각 이웃의 embedding들에 행렬 W를 곱하고 벡터 b를 더한 후 max-pooling을 하는 방법입니다.
▶ GNN과 CNN의 유사점/차이점
- 유사점 : 두 신경망 모두 이웃의 정보를 aggregate하는 방식입니다. GNN은 이웃노드의 정보를, CNN은 이웃 픽셀의 정보를 aggregate합니다.
- 차이점 : CNN은 필터의 크기가 일정하기 때문에 이웃의 수가 균일하지만, GNN에서는 노드별로 이웃의 수가 다릅니다.
=> 그렇다면, 그래프의 연결 정보를 담고 있는 인접 행렬에 CNN을 적용하면 효과적일까요?
답은 '아니다' 입니다. CNN이 주로 사용되는 이미지 같은 경우에는 인접 픽셀이 유용한 정보를 갖고 있을 확률이 높습니다. 그러나 그래프의 경우에 이웃 노드는 제한된 정보만을 가지며, 인접행렬의 순서가 임의로 결정된다는 점 때문에 정보의 유용성이 떨어집니다.
▶ GNN의 한계
GNN에서는 이웃 노드드의 정보를 동일한 가중치로 평균을 냅니다. GCN도 마찬가지로 단순히 연결성을 고려한 가중치로 평균을 냅니다. 그러나 실세계에서는 모든 이웃 노드들이 동등하게 중요하고, 동등한 역할을 하지는 않습니다. 실제 그래프에서는 이웃 노드별로 미치는 영향이 다를 수 있음을 고려해야 합니다. 이를 해결한 것이 그래프 어텐션 신경망(Graph Attention Network, GAT)입니다. GAT는 이웃과의 가중치 자체도 학습합니다. 이 과정에서 self attention이 사용됩니다.
'AI Research > Deep Learning' 카테고리의 다른 글
| [딥러닝 기본지식] 딥러닝 프레임워크 비교(Tensorflow, Keras, Pytorch) (0) | 2023.03.04 |
|---|---|
| [딥러닝 기본지식] Transfer Learning과 Fine Tuning (0) | 2023.03.04 |
| [딥러닝 기본지식] 가중치(weight)와 편향(bias) (0) | 2023.03.04 |
| [딥러닝 기본지식] 평가 지표(Metrics) (0) | 2023.03.04 |
| [딥러닝 기본지식] 오차 역전파(backpropagation)의 이해 - 계산그래프와 연쇄법칙(chain rule) (1) | 2023.03.04 |