논문 링크: https://arxiv.org/pdf/1801.07698.pdf
Github: https://github.com/ronghuaiyang/arcface-pytorch
GitHub - ronghuaiyang/arcface-pytorch
Contribute to ronghuaiyang/arcface-pytorch development by creating an account on GitHub.
github.com
- Abstract
최근 얼굴인식 분야에서 데이터 집합의 클래스들 사이의 거리를 최대화 하기 위해 softmax 함수에 margin을 추가하는 방법을 사용하고 있습니다. 이를 통해 얼굴인식 분야에서 discriminative한 feature를 얻을 수 있다고 합니다.
본 논문에서는 hypersphere에서의 geodesic distance(두 점을 잇는 최단 거리)와 정확히 일치하기 때문에 기하학적으로 해석이 명확하다고 할 수 있고 , 이를 통해 모델의 분별력을 향상시키는 Additive Angular Margin Loss(ArcFace)를 소개하고 있습니다.
1. Introduction
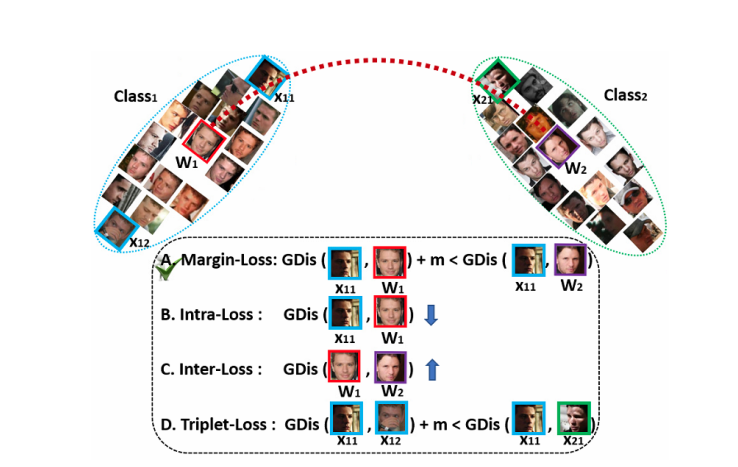
얼굴 인식 분야에서 Deep CNN을 학습시키기 위해 사용하는 방법에는 크게 두 가지가 존재합니다. 첫 번째는 softmax loss를 사용하는 것과 두 번째는 embedding을 직접 학습하는 triplet loss를 사용하는 방법입니다. 하지만 이 두 방법 모두 몇 가지 단점이 존재합니다.
- softmax loss: 학습 feature들이 closed-set(test set의 class들이 train set에 있는 경우, 일반적인 딥러닝에서의 분류 문제)에 대해서는 잘 분류하지만 open-set(test set의 class들이 train set에 없는 경우)에 대해서는 잘 분류하지 못합니다. 또한 선형 변환 행렬이 클래수 갯수 N에 따라서 선형적으로 증가하게 됩니다.
- triplet loss: 대규모 데이터 집합에서 triple 조합의 수(기준점, positive, negative anchor)가 폭발적으로 증가하게 되고 이는 반복 횟수에도 엄청난 증가를 가져옵니다. 또한 이 조합에 따라 성능차이가 발생하기 때문에 효과적인 모델 학습을 어렵게 만듭니다.
이러한 단점을 해결하고 margin이 주는 효과를 이용하기 위해 softmax loss에 margin penalty를 통합하는 방식이 사용되고 있습니다.
따라서 본 논문에서는 학습 과정을 안정화하고 모델의 식별력을 높히기 위해 Additive Angular Margin Loss(ArcFace)를 제안합니다. 구체적으로, Deep CNN의 feature와 마지막 fully connected layer 사이의 내적은 feature와 center normalization 후 코사인 거리와 같습니다. arc-cosine 함수를 사용하여 현재 feature와 target 사이의 각도를 계산합니다. 그런 다음 목표 각도에 추가 angular margin을 도입하고 코사인 함수로 다시 target logit을 얻습니다. 그런 다음 고정된 feature norm으로 모든 logit을 다시 조정하는데 이는 softmax 손실과 정확히 동일합니다. 정규화된 hypersphere에서 각도와 호(arc) 사이의 정확한 대응으로 인해 우리의 방법은 거리 margin을 직접 최적화할 수 있으므로 이를 ArcFace라고 합니다.
논문에서 제안하는 ArcFace의 장점은 다음과 같습니다!
- Intuitive : 정규화된 hypersphere에서 angle과 arc사이의 정확한 일치 덕분에(hypersphere 가 구이기 때문에 반지름이 모두 같아 호는 각도의 영향만 받습니다.) geodesic distance margin을 직접적으로 최적화 할 수 있습니다.
- Economical : sub-center ArcFace 는 큰 비용 없이 noise 데이터에 대응할 수 있습니다.
- Easy : 간단한 코드 몇 줄로 구현할 수 있으며, 다양한 딥러닝 프레임 워크에서 작동 가능합니다.
- Efficient: 학습 단계에서 무시 가능한 정도의 계산 복잡도만이 추가됩니다.
- Effective : IBUG-500K 데이터를 이용해 sota를 달성했습니다.
- Engaging : discriminative power와 generative power 모두 개선 가능합니다.
2. Proposed Approach
아래 식은 기존에 많이 사용하던 softmax loss 함수의 수식입니다.
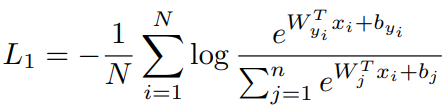
우리의 목표는 intra-class(동일 클래스)들 끼리는 비슷하게 임베딩 되고, inter-class(서로 다른 클래스)들 끼리는 다르게 임베딩되는 것입니다. 하지만 face recognition task는 모두 '사람'으로 구성된 데이터들을 구별해야 하고 이는 intra-class와 동일합니다. 다시 말해, 같은 클래스내의 데이터들의 임베딩이 서로 유사하게, 다른 클래스 상의 임베딩이 서로 다르고 다양하게 임베딩 되도록 최적하지 못하는 것입니다. 이러한 이유 때문에 face recognition에서 softmax 사용시 성능 저하가 발생하기도 합니다.
위 softmax loss의 문제를 해결하기 위해 본 논문에서는 각도에 집중하는 방법을 제안 합니다.
위 식을 간단히 하기 위해 먼저 bias 를 0으로 두겠습니다. 그 다음 기존의 logit에 해당하던 Wx를 아래 식으로 수정합니다.
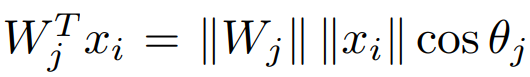
위 식에서
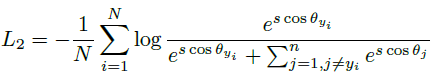
이제 이 개념들을 적용하여 ArcFace loss가 cross entropy에 반영되어 학습하는과정을 알아보겠습니다.
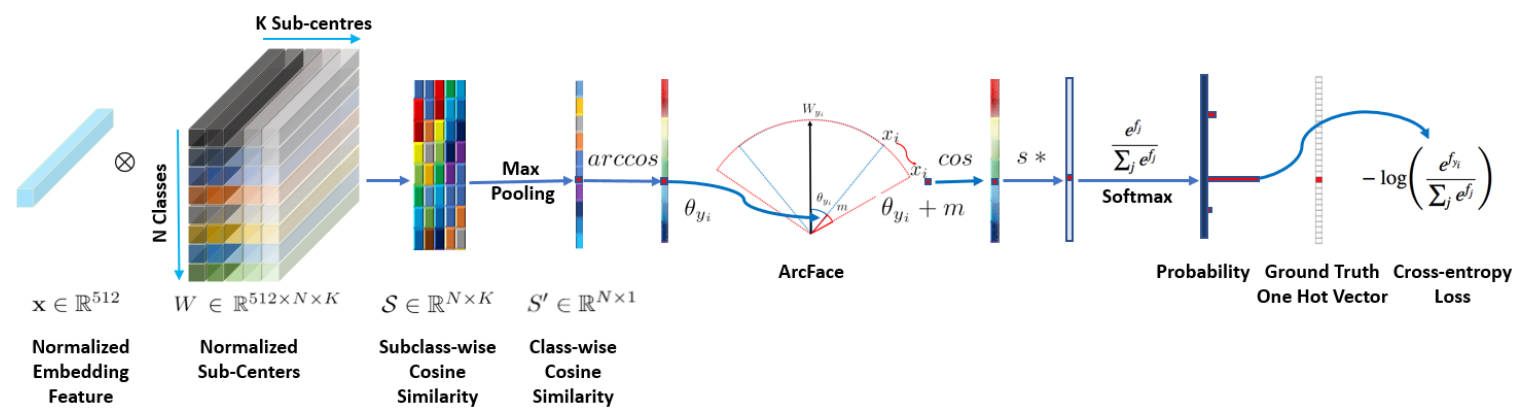
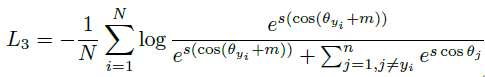
L: loss
N: batch size
m: margin (각도에 직접 margin을 더해줌으로써 거리에 따라 패널티를 부여합니다.)
s: scale
θ: 임베딩 벡터와 정답 클래스 사이의 각도
1. 클래스별 정답 임베딩 벡터와 분류기를 거친 후의 feature(logit) 사이의 코사인 유사도를 통해 , cos θ를 구합니다. (코사인 유사도의 값이 클수록 두 벡터 사이의 각도가 작은 것입니다. 정답에 가깝게 logit을 구해낸 것)
2. arccos함수를 이용해 두 벡터사이의 각도인 θ를 구합니다.
3. θ에 margin을 더해 cos(θ+m)을 구합니다. 동일 클래스들끼리는 모이고, 서로 다른 클래스들 끼리는 멀어질 수 있도록 두 벡터 사이에 margin을 더해줍니다. 이는 intra-class 내에서는 compactness를 증가시키고, inter-class 사이에서는 discrepancy를 증가시키는 효과를 얻을 수 있습니다.
4. 3에서 얻은 cos(θ+m)으로 softmax를 구합니다. 정답 벡터와 임베딩 벡터 사이가 가까울 수록 각도 θ가 작아지므로 cosθ의 값은 커지게 됩니다. 따라서 softmax값도 커집니다.
5. 4에서 얻은 값을 새로운 logit으로 하여 cross entropy를 구합니다.
(cross entropy loss의 특성은 정답 class의 softmax값은 1에 가까워지게 하고, 정답이 아닌 class에 해당하는 softmax의 값은 0에 가깝게 만듭니다. 이를 각도의 개념에서 보면, 정답에 해당하는 class의 softmax값 이 1에 가까워지게 해서 class의 중심과 입력 사이의 각도가 0에 가까워지게 만들고 (cos0 = 1 이므로) , 그 반대의 경우는 0에 가까워지게 해서 다른 class의 중심과 입력 간의 각도가 멀어지도록 학습이 가능한 것입니다. )
이렇게 학습 하였을 경우 softmax와 비교했을 때 class들 사이의 명백한 gap을 가지게 된다고 설명합니다.
위 그림에서 점은 데이터 하나하나를 의미하고, 선은 각 class의 중심방향을 의미합니다. l2 normalization을 사용함으로써 모든 feature들이 일정한 반지름 값을 가지는 구의 공간에 존재합니다.
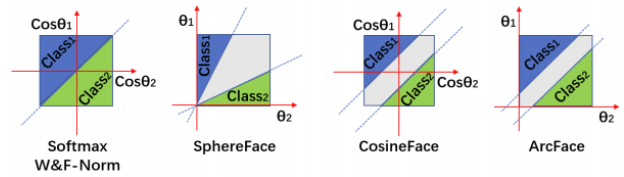
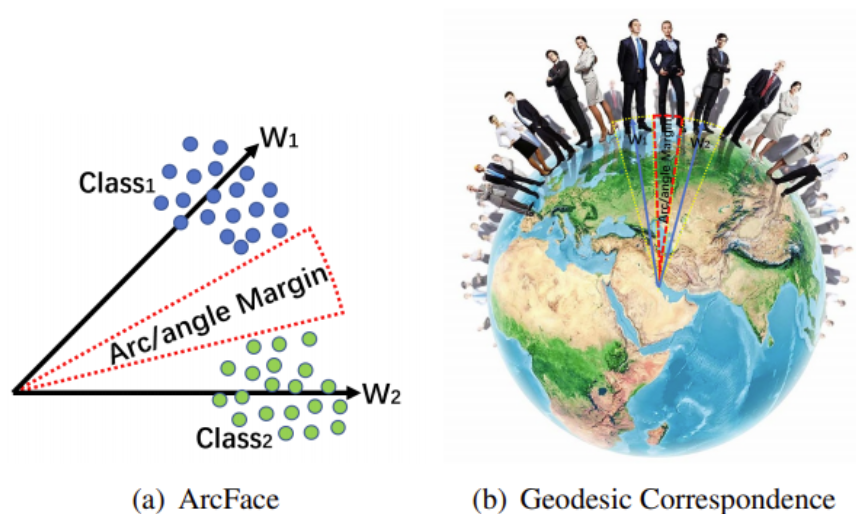
동일한 class들 사이의 geodesic distance는 margin을 추가했을 때 더 분명해지는 것을 확인할 수 있습니다.